Teoreme de Bernoulli
El Teorema de Bernoulli es un caso particular de la Ley de los grandes números, que precisa la aproximación frecuencial de un suceso a la probabilidad p de que este ocurra a medida que se va repitiendo el experimento.
|
El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una línea de corriente. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:
- Cinética: es la energía debida a la velocidad que posea el fluido.
- Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
- Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.
La siguiente ecuación conocida como "Ecuación de Bernoulli" (Trinomio de Bernoulli) consta de estos mismos términos.

- V = velocidad del fluido en la sección considerada.
- g = aceleración gravitatoria
- z = altura en la dirección de la gravedad desde una cota de referencia.
- P = presión a lo largo de la línea de corriente.
- ρ = densidad del fluido.
- Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona 'no viscosa' del fluido.
- Caudal constante
- Flujo incompresible, donde ρ es constante.
- La ecuación se aplica a lo largo de una línea de corriente o en un flujo irrotacional
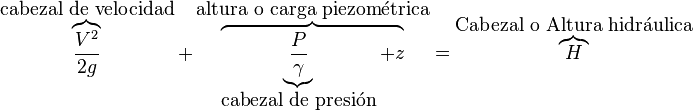

- q + p = p0
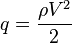
- p = P + γz
- p0 es una constante-

donde:
Para aplicar la ecuación se deben realizar los siguientes supuestos:
Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.
Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.
Características y consecuencias
Cada uno de los términos de esta ecuación tienen unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término z se suele agrupar con P / γ para dar lugar a la llamada altura piezométrica o también carga piezométrica.
También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por γ, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
o escrita de otra manera más sencilla:
donde
Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:
Ecuación de Bernoulli y la Primera Ley de la Termodinámica

Demostración
Escribamos la primera ley de la termodinámica con un criterio de signos termodinámico conveniente:

Recordando la definición de la entalpía h = u + Pv, donde u es la energía interna y v se conoce como volumen específico v = 1 / ρ. Podemos escribir:

que por la suposiciones declaradas más arriba se puede reescribir como:

dividamos todo entre el término de la aceleración de gravedad

Aplicaciones del Principio de Bernoulli
Airsoft
Chimenea
Tubería
Natación
Movimiento de una pelota o balón con efecto
Carburador de automóvil
Flujo de fluido desde un tanque
Dispositivos de Venturi

 un número positivo cualquiera, la probabilidad de que la frecuencia relativa f/n discrepe de p en más de
un número positivo cualquiera, la probabilidad de que la frecuencia relativa f/n discrepe de p en más de 

